Validity
In logic, an argument is valid if and only if its conclusion is a logical consequence of its premises, a formula is valid if and only if it is true under every interpretation, and an argument form (or schema) is valid if and only if every argument of that logical form is valid.
Contents |
Validity of arguments
An argument is valid if and only if the truth of its premises entails the truth of its conclusion. It would be self-contradictory to affirm the premises and deny the conclusion. The corresponding conditional of a valid argument is a logical truth and the negation of its corresponding conditional is a contradiction. The conclusion is a logical consequence of its premises.
An argument that is not valid is said to be “invalid”.
An example of a valid argument is given by the following well-known syllogism (also known as modus ponens):
- All men are mortal.
- Socrates is a man.
- Therefore, Socrates is mortal.
What makes this a valid argument is not that it has true premises and a true conclusion, but the logical necessity of the conclusion, given the two premises. The argument would be just as valid were the premises and conclusion false. The following argument is of the same logical form but with false premises and a false conclusion, and it is equally valid:
- All cups are green.
- Socrates is a cup.
- Therefore, Socrates is green.
No matter how the universe might be constructed, it could never be the case that these arguments should turn out to have simultaneously true premises but a false conclusion. The above arguments may be contrasted with the following invalid one:
- All men are mortal.
- Socrates is mortal.
- Therefore, Socrates is a man.
In this case, the conclusion does not follow inescapably from the premises. All men are mortal, but not all mortals are men. Every living creature is mortal; therefore, even though both premises are true and the conclusion happens to be true in this instance, the argument is invalid.
A standard view is that whether an argument is valid is a matter of the argument’s logical form. Many techniques are employed by logicians to represent an argument’s logical form. A simple example, applied to two of the above illustrations, is the following: Let the letters ‘P’, ‘Q’, and ‘S’ stand, respectively, for the set of men, the set of mortals, and Socrates. Using these symbols, the first argument may be abbreviated as:
- All P are Q.
- S is a P.
- Therefore, S is a Q.
Similarly, the third argument becomes:
- All P are Q.
- S is a Q.
- Therefore, S is a P.
An argument is formally valid if its form is one such that for each interpretation under which the premises are all true, the conclusion is also true. As already seen, the interpretation given above does cause the second argument form to have true premises and false conclusion, hence demonstrating its invalidity.
Valid formula
A formula of a formal language is a valid formula if and only if it is true under every possible interpretation of the language.
Validity of statements
A statement can be called valid, i.e. logical truth, if it is true in all interpretations.
For example: If no god is mortal, then no mortal is a god.
In logical form, this is:
- If no P is Q, then no Q is P.
A given statement may be entailed by other statements, i.e. the given statement must be true if the other statements are true. This means that an argument with the given statement as its conclusion and the other statements as its premises is a valid argument. The corresponding conditional of a valid argument is a logical truth.
Validity and soundness
Validity of deduction is not affected by the truth of the premise or the truth of the conclusion. The following deduction is perfectly valid:
- All fire-breathing rabbits live on Mars
- All humans are fire-breathing rabbits
- Therefore all humans live on Mars
The problem with the argument is that it is not sound. In order for a deductive argument to be sound, the deduction must be valid and all the premises true.
Satisfiability and validity
Model theory analyzes formulae with respect to particular classes of interpretation in suitable mathematical structures. On this reading, formula is valid if all such interpretations make it true. An inference is valid if all interpretations that validate the premises validate the conclusion. This is known as semantic validity.[1]
Preservation
In truth-preserving validity, the interpretation under which all variables are assigned a truth value of 'true' produces a truth value of 'true'.
In a false-preserving validity, the interpretation under which all variables are assigned a truth value of ‘false’ produces a truth value of ‘false'.[2]
-
Preservation properties Logical connective sentences True and false preserving: Logical conjunction (AND, 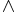 ) • Logical disjunction (OR,
) • Logical disjunction (OR, 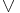 )
)True preserving only: Tautology ( 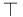 ) • Biconditional (XNOR,
) • Biconditional (XNOR,  ) • Implication (
) • Implication (  ) • Converse implication (
) • Converse implication (  )
)False preserving only: Contradiction (  ) • Exclusive disjunction (XOR,
) • Exclusive disjunction (XOR,  ) • Nonimplication (
) • Nonimplication ( 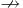 ) • Converse nonimplication (
) • Converse nonimplication ( 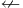 )
)Non-preserving: Proposition • Negation ( 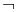 ) • Alternative denial (NAND,
) • Alternative denial (NAND,  ) • Joint denial (NOR,
) • Joint denial (NOR,  )
)
n-Validity
A formula A of a first order language 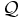 is n-valid iff it is true for every interpretation of
is n-valid iff it is true for every interpretation of 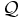 that has a domain of exactly n members.
that has a domain of exactly n members.
ω-Validity
A formula of a first order language is ω-valid iff it is true for every interpretation of the language and it has a domain with an infinite number of members.
See also
References
- Barwise, Jon; Etchemendy, John. Language, Proof and Logic (1999): 42.
- Beer, Francis A. "Validities: A Political Science Perspective", Social Epistemology 7, 1 (1993): 85-105.